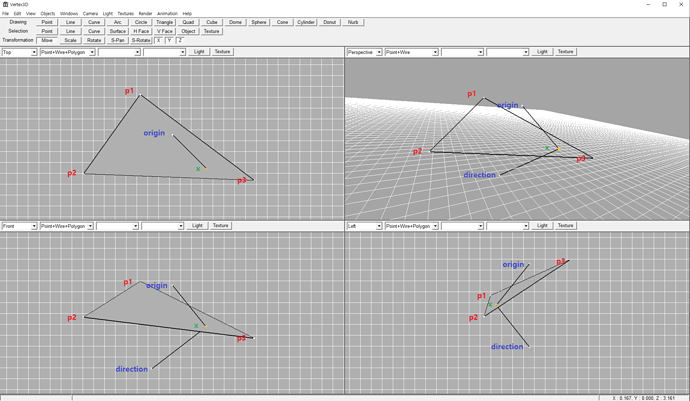
Hi,
Actually I have previous post open but would like to ask one more thing here.
- Previous one: In regard to Ray Triangle Intersection
I’ve tried various Ray Triangle Intersection algorithms and found that it works with some conditions but some doesn’t.
For example, the line is passing through triangle if you check out below screenshot, but algorithm returns false if the direction changes
- Case 1
Origin → Direction: Function IntersectTriangle returns true
- Case 2
Direction → Origin: Function IntersectTriangle returns false
I would like to have your advice to solve following problems in my program.
- Incorrect coordinate of intersection point x
- Reason why Ray Triangle Intersection algorithm returns different result when the direction of line gets changed?
struct Ray {
vec3 Origin;
vec3 Dir;
};
// Check whether the intersect point is in triangle
bool PointInOrOn(vec3 p1, vec3 p2, vec3 a, vec3 b) {
// if the line from a corner point to the intersection point is between the to legs which are connected to the corner point
vec3 cp1 = cross(b - a, p1 - a);
vec3 cp2 = cross(b - a, p2 - a);
// Return its result
return dot(cp1, cp2) >= 0;
}
// Check whether the point is in triangle
bool PointInTriangle(vec3 px, vec3 p1, vec3 p2, vec3 p3) {
return PointInOrOn(px, p1, p2, p3) && PointInOrOn(px, p2, p3, p1) && PointInOrOn(px, p3, p1, p2);
}
// Check intersection point
vec3 IntersectPlane(Ray ray, vec3 p1, vec3 p2, vec3 p3) {
// Direction
vec3 D = ray.Dir;
// The normal vector of the plane can be calculated by the cross product of 2 legs of the triangle
vec3 N = cross(p3 - p1, p2 - p1);
// The intersection point X
vec3 x = ray.Origin + D * dot(p1 - ray.Origin, N) / dot(D, N);
// Return coordinate of intersect point
return x;
}
// Check intersection between given line and triangle + obtain coordinate of intersect point
bool IntersectTriangle(Ray ray, vec3 p1, vec3 p2, vec3 p3, vec3 &x) {
// Get coordinate of intersect point
x = IntersectPlane(ray, p1, p2, p3);
// Check intersection
return PointInTriangle(X, p1, p2, p3);
}
// Main
int main() {
// Intersection point
vec3 x = vec3(0.0, 0.0, 0.0);
// Triangle
vec3 p1 = vec3(2.1, 3.0, 0.4);
vec3 p2 = vec3(-0.5, 1.3, 4.0);
vec3 p3 = vec3(7.0, 0.4, 4.3);
// Line (Original)
Ray ray;
ray.Origin = vec3(3.6, 2.8, 2.3);
ray.Dir = vec3(2.7, -1.0, 2.2);
// Intersection check + obtain coordinate of intersection point
bool rt = IntersectTriangle(ray, p1, p2, p3, x); // Return true
// Line (Reverse)
ray.Origin = vec3(2.7, -1.0, 2.2);
ray.Dir = vec3(3.6, 2.8, 2.3);
// Intersection check + obtain coordinate of intersection point
rt = IntersectTriangle(ray, p1, p2, p3, x); // Return false
return 0;
}