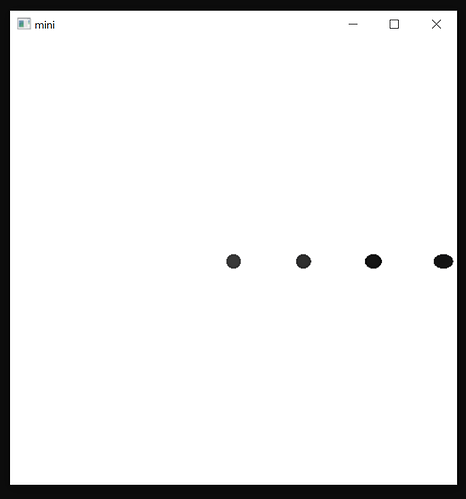
I have a ray tracer in GLSL which is rendering a stretched image near the border of the screen (refer to the attached screenshot). I have tried to render the direction of the ray as a colour directly from the vertex shader and I did not observer any faster shifts so the ray direction seems to be output correctly. The math of the ray march also looks good. I cannot figure out why the spheres are stretched.
Here is a working code which showcases the problem.
const char* vertex_shader = R"Vertex_Shader(
#version 300 es
precision mediump float;
layout (location = 0) in vec2 v_position;
out vec3 f_ray_position;
out vec3 f_ray_direction;
void main()
{
gl_Position = vec4(v_position, 0.0f, 1.0f);
f_ray_position = vec3(0.0f, 0.0f, -16.0f);
f_ray_direction = v_position.x * vec3(1.0f, 0.0f, 0.0f)
+ v_position.y * vec3(0.0f, 1.0f, 0.0f)
+ vec3(0.0f, 0.0f, 1.0f);
}
)Vertex_Shader";
const char* fragment_shader = R"Fragment_Shader(
#version 300 es
precision mediump float;
in vec3 f_ray_position;
in vec3 f_ray_direction;
out vec4 fragment_colour;
struct Sphere {
vec3 origin;
float radius;
};
Sphere[4] spheres = Sphere[4](
Sphere(vec3(0.0f, 0.0f, 0.0f), 0.5f),
Sphere(vec3(5.0f, 0.0f, 0.0f), 0.5f),
Sphere(vec3(10.0f, 0.0f, 0.0f), 0.5f),
Sphere(vec3(15.0f, 0.0f, 0.0f), 0.5f)
);
vec3 march(vec3 origin, vec3 direction)
{
bool hit = false;
vec3 position = origin;
float total_distance = 0.0f;
for (uint steps = 0u; steps < 30u && !hit; ++steps)
{
float distance = 10000.0f;
for (int i = 0; i < 4; ++i)
{
vec3 position = origin + direction * total_distance;
float sphere_distance = length (position - spheres[i].origin) - spheres[i].radius;
distance = min(distance, sphere_distance);
}
total_distance += distance;
hit = 0.000001f > distance;
}
return vec3(1.0f) - (total_distance / 20.0f);
}
void main()
{
vec3 colour = march(f_ray_position, normalize (f_ray_direction));
fragment_colour = vec4(abs(colour), 1.0f);
}
)Fragment_Shader";
#include <math.h>
#include <stdio.h>
#include <GL/glew.h>
#include <GL/glut.h>
GLuint vao;
GLuint vbo;
GLuint program;
void onDisplay(void)
{
glViewport(0, 0, (GLsizei)500, (GLsizei)500);
glClearColor(0.3f, 0.3f, 0.3f, 0.0f);
glClear(GL_COLOR_BUFFER_BIT);
glUseProgram(program);
glBindVertexArray(vbo);
glDrawArrays(GL_TRIANGLES, 0, 6);
glBindVertexArray(vbo);
glutSwapBuffers();
}
void printError(const char* context)
{
GLenum error = glGetError();
if (error != GL_NO_ERROR) {
fprintf(stderr, "%s: %s\n", context, gluErrorString(error));
};
}
GLfloat vertices[] = {
1, 1,
1, -1,
-1, -1,
1, 1,
-1, -1,
-1, 1
};
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize(500, 500);
glutCreateWindow("mini");
glewExperimental = GL_TRUE;
glewInit();
GLuint vertexShader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(vertexShader, 1, &vertex_shader, NULL);
glCompileShader(vertexShader);
GLuint fragmentShader = glCreateShader(GL_FRAGMENT_SHADER);
glShaderSource(fragmentShader, 1, &fragment_shader, NULL);
glCompileShader(fragmentShader);
program = glCreateProgram();
glAttachShader(program, vertexShader);
glAttachShader(program, fragmentShader);
glLinkProgram(program);
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
glEnableVertexAttribArray(0);
glVertexAttribPointer(0, 2, GL_FLOAT, GL_FALSE, sizeof(float) * 2, 0);
glBindVertexArray(0);
glutDisplayFunc(onDisplay);
glutMainLoop();
glBindBuffer(GL_ARRAY_BUFFER, 0);
glDeleteBuffers(1, &vbo);
glBindVertexArray(0);
glDeleteVertexArrays(1, &vao);
glDetachShader(program, vertexShader);
glDetachShader(program, fragmentShader);
glDeleteProgram(program);
glDeleteShader(vertexShader);
glDeleteShader(fragmentShader);
return 0;
}