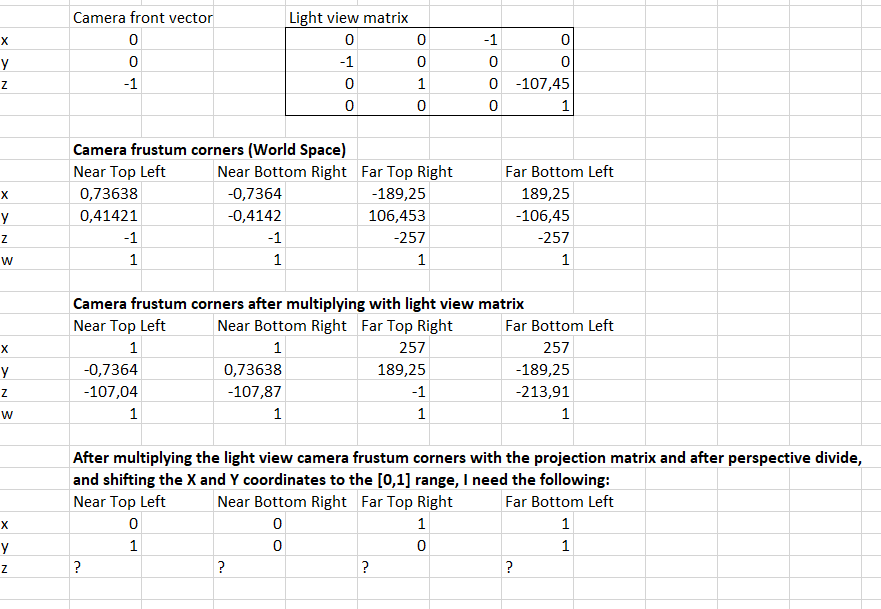
I’m trying to rectify a shadow map using the matrix multiplication technique that is introduced in Section 4.2 of Filter-based Real-time Single Scattering using Rectified Shadow Maps (Klehm et al., 2014). In short, the idea is to have a light view matrix that has the camera 3D bisectrix coming in from the left-hand side, and a light projection matrix that projects view rays so that they are parallel to each other. The projection matrix can be obtained using the common projection matrix with the near/far, left/right and top/bottom parameters and then using the coordinates of the camera frustrum corners as the actual parameters.
The problem I’m currently having is that I haven’t been able to find the correct parameter values for the common projection matrix that actually give me proper rectificiation, as positions on the same epipolar slice currently do not have the same Y-coordinate after projection, and since points on the camera near or far plane currently do not have the X-coordinate 0 or 1 respectively. I almost start to believe that there is no projection matrix that results in the proper rectification after trying all kinds of combinations of parameters, but I’m probably doing something wrong. The aforementioned paper mentions that the bisectrix causes the left/right (side planes, “y axis”) to have the same absolute value and that a projective transformation is performed along x, thus that the camera frustum corners’ minimal and maximal X-coordinates should be used for the near and far parameters. The top/bottom values should then be obtained with the minimal and maximal Z-coordinates of the camera frustum corners. Also since the paper is about directional lights mostly, I assume that an orthographic projection matrix is used, but it may be possible with a perspective projection matrix as well.
Even with this information, I have not succeeded in finding the correct values that give me proper epipolar rectification. I have included an image that shows information about a simple situation for which I tried to find the correct projection matrix (camera frustum corners and light view matrix are given). Do you know what values I should use for the projection matrix, or what I might be doing wrong?