What method can be used to map pixel coordinates into a geometric coordinate range?

[mirro187]

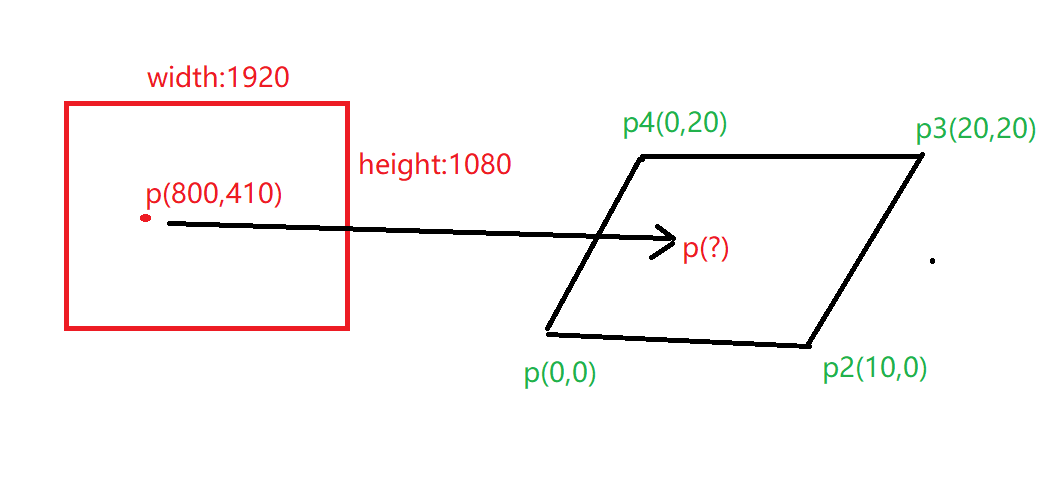
env win10&gtx3050ti&opengl4.0

[carsten_neumann]

With the information you’ve provided all I can say is:

• presumable you somehow map the quadrilateral on the right to an area of your screen (or is it a texture?) on the left
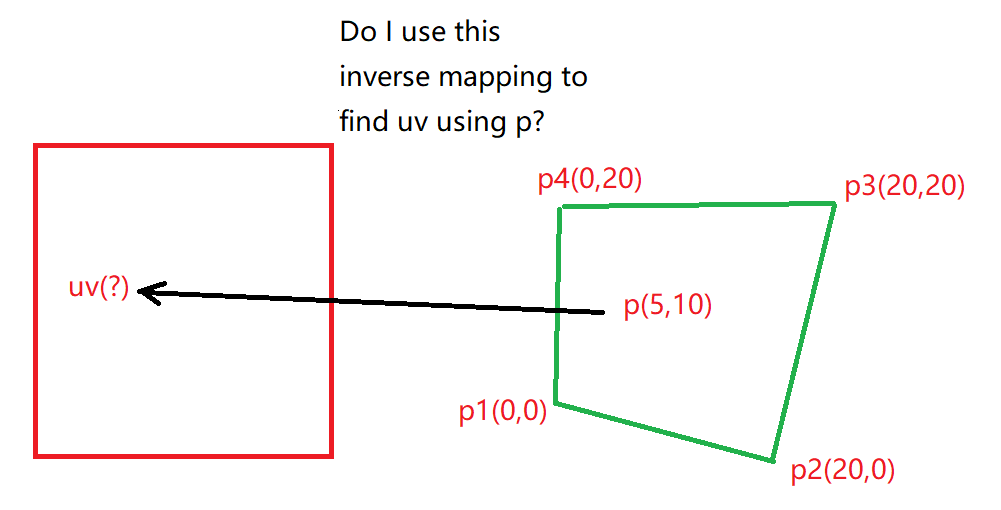
• the inverse of that mapping is what you are looking for

Taking a wild guess you may be looking for the functionality of glm::unproject or gluUnProject?

[GClements]

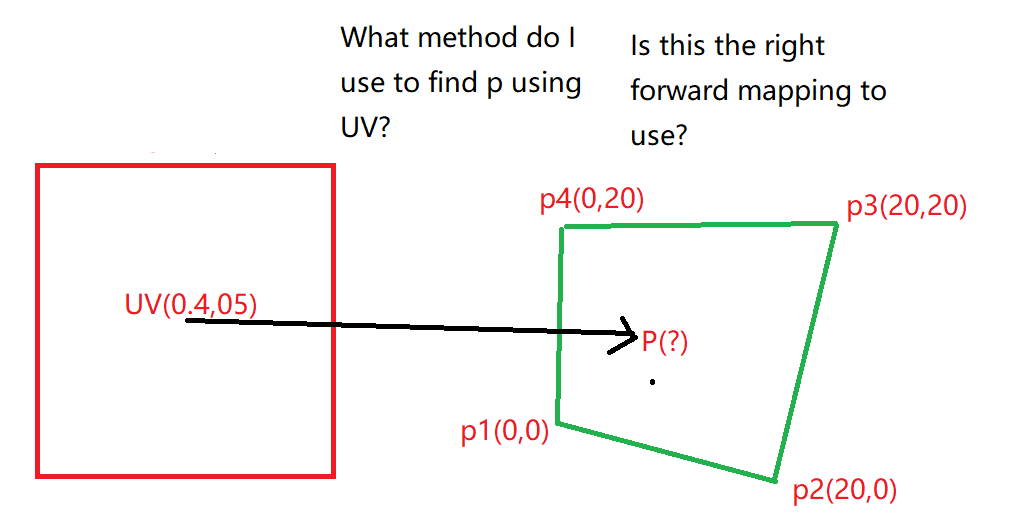
The forward mapping is straightforward:

p = mix(mix(p1,p2,u),mix(p4,p3,u),v);

Where mix(a,b,t) = (1-t)a+tb = a+t(b-a) and u,v are in [0,1] (so u=x/width, v=y/height).

For the inverse mapping, if you expand out the forward mapping you get a pair of bilinear equations. Solve one for u, substitute into the second to get a quadratic in v, solve using the quadratic formula, substitute back into the first to get u (or repeat the process, solving the first for v then the second for u). You’ll want to use a computer algebra system (Mathematica, Wolfram Alpha, etc); it’s too messy to solve by hand. Or search for “inverse bilinear mapping”.

[mirro187]

Is the following url a forward mapping?

Quadrilateral Interpolation, Part 2 – Nathan Reed’s coding blog

Is the following url a inverse mapping?

Inigo Quilez

God, I only know how to do math. Can you confirm that for me or Are there any open source libraries available?

[GClements]

Both of those start with the forward mapping and demonstrate how to invert it.

[mirro187]

Do I mapping from pixel coordinate to geometric coordinate using a forward method?If I use the inverse mapping,Is the following call correct?

vec2 geoPos = invBilinear(p(800,410), in vec2(0,0), vec2(10,0), vec2(20,20), vec2(0,20))

float cross( in vec2 a, in vec2 b ) { return a.x*b.y - a.y*b.x; }

vec2 invBilinear( in vec2 p, in vec2 a, in vec2 b, in vec2 c, in vec2 d )
{
    vec2 res = vec2(-1.0);

    vec2 e = b-a;
    vec2 f = d-a;
    vec2 g = a-b+c-d;
    vec2 h = p-a;
        
    float k2 = cross2d( g, f );
    float k1 = cross2d( e, f ) + cross2d( h, g );
    float k0 = cross2d( h, e );
    
    // if edges are parallel, this is a linear equation
    if( abs(k2)<0.001 )
    {
        res = vec2( (h.x*k1+f.x*k0)/(e.x*k1-g.x*k0), -k0/k1 );
    }
    // otherwise, it's a quadratic
    else
    {
        float w = k1*k1 - 4.0*k0*k2;
        if( w<0.0 ) return vec2(-1.0);
        w = sqrt( w );

        float ik2 = 0.5/k2;
        float v = (-k1 - w)*ik2;
        float u = (h.x - f.x*v)/(e.x + g.x*v);
        
        if( u<0.0 || u>1.0 || v<0.0 || v>1.0 )
        {
           v = (-k1 + w)*ik2;
           u = (h.x - f.x*v)/(e.x + g.x*v);
        }
        res = vec2( u, v );
    }
    
    return res;
}

[GClements]

@mirro187

Do I mapping from pixel coordinate to geometric coordinate using a forward method?

What exactly are you trying to do? If you’re implementing bilinear texture mapping, you’d normally use an inverse mapping using the positional coordinates followed by a forward mapping using the texture coordinates. If the texture coordinates are the unit square, you can omit the forward mapping.

[mirro187]

Thank you for your reply. Is the schematic diagram below clear?