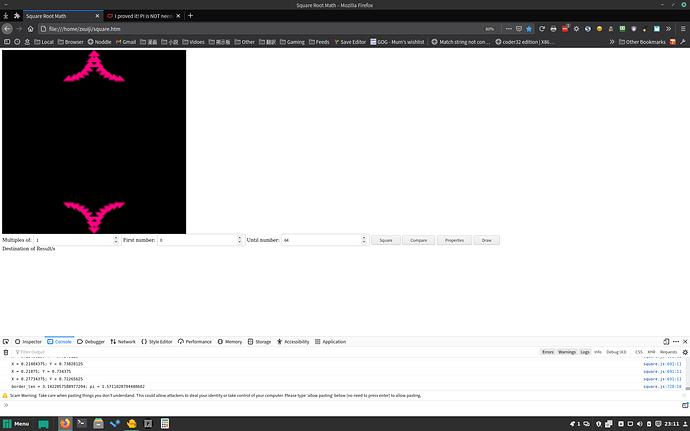
I got my curve without PI! Sadly it didn’t result in a circle because the curves went opposite direction to what I expected however they DID curve. For now I’ll leave this topic open for a couple days as I won’t have time to cleanup the code and slap a license on it with all the overtime I will be doing but I will do so during the holidays I booked off during the upcoming week.
You don’t need pi to make a curve. You do need some function of pi or trigonometry to compute an actual circle. Circles are curves, but not all curves are circles.
You don’t get it, I generated normalized values in a loop and drew 4 different curves just by switching between positive and negative, in other words circles & curves math never needed trigonometry, you’ll see what I mean when I upload the code to my github account in 2 days time.
That sounds like you “discovered” finite serieses that approximate trig functions. Which we’ve known about for centuries.
You still don’t get it, trigonometry uses angles, my method doesn’t use that, it directly calculates the x & y values of each point, the only divisions needed are before the loop for getting normalized values to judge how far apart each point should be
what you did is most probably much less brilliant than you thought it would be.
In case you aren’t aware, it’s fairly common to represent circles using rational Bezier curves or NURBS. E.g.:
#define k
const float k = 0.7071067811865476; // = 1/sqrt(2)
float points[3][4] = {
{0, 1, 0, 1},
{k, k, 0, k}, // i.e. (1,1,0) with "weight" 1/sqrt(2)
{1, 0, 0, 1}
};
glEnable(GL_MAP1_VERTEX_4);
glMap1f(GL_MAP1_VERTEX_4, 0.0, 1.0, 4, 3, points[0]);
glMapGrid1f(count, 0, 1);
glEvalMesh1(GL_LINE, 0, count);
will draw a 90° circular arc. This corresponds to the equations:
x = ((√2-1)t2-(√2)t)/((√2-2)t2+(2-√2)t-1)
y = ((√2-1)t2+(2-√2)t-1)/((√2-2)t2+(2-√2)t-1)
You can use a CAS to verify that this satisfies x2+y2=1.
You only need to use sin/cos if you want the points to be evenly-spaced.
More generally, you can make an arc of any angle less than 180° using a rational quadratic curve. The first and last points are the endpoints, the middle point is the point of intersection of the tangents, projected so that its w coordinate is cos(θ/2), where θ is the angle subtended by the arc. Smaller arcs will result in more evenly spaced points.
This follows from the fact that a circle is a cone in homogeneous coordinates, so any curve which lies on that cone will be a circular arc after projective division. The intersection of a cone with a plane parallel to any tangent plane is a parabola, which is a quadratic curve.
PS: With a degree-5 curve, i.e. 6 control points, you can make a complete circle from a single segment:
(0,0,1), (4,0,1)/5, (2,4,1)/5, (-2,4,1)/5, (-4,0,1)/5, (0,0,1)
(Z coordinate omitted).
Yeaahhh, using sqrt per coordinate is slow compared to mine, mine just does a few additions and subtractions per coordinate (unless you count multiplying against the boolean result of a comparison to avoid branching), there is no guess work involved in the calculations - unless you count me trying to figure out how to offset the curves to the right place since at the moment I get the following:
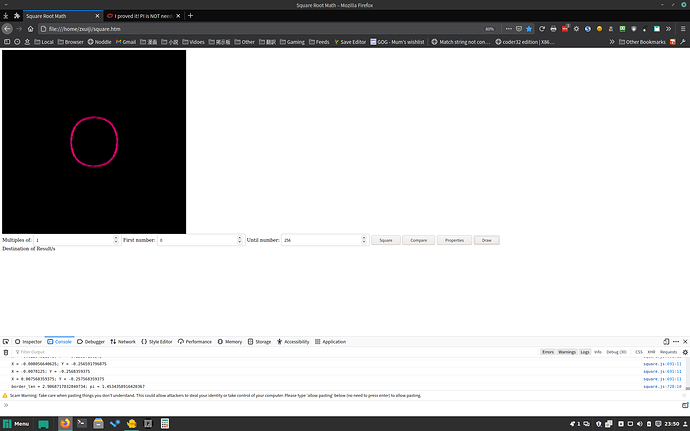
The only division that occurs is before the loop begins, every calculation within the loop is essentially just an increment/decrement in behaviourManaged to resolve the offset problem, looks a LOT closer to a circle now, next is perhaps stopping early cause it slightly looks squarish
Edit: Aaaand now I have a rough idea of how to calculate PI without the circumference, though the formula itself needs fine tuning as the current version uses a hard coded number, a number of which I need to somehow acquire in code
Well that sucks, while I was modifying the license to include license fees there was a power cut and now my system won’t boot, will see what I can do about uploading code from a live USB for now, work on the system part after
Edit: 2nd power cut just occured, I get the feeling I’m not gonna get it uploaded today as I was planning, I’ll give up for now and try a few hours later
You want to charge licensing fees for an algorithm to approximate circles and arcs? I’m not sure that’s viable (outside of getting a patent, and there’s almost certainly prior art out there for it), but good luck with that.
Phew, finally finished rearranging my living room while waiting out those few hours, now just got the problem of a lack of screen when I boot up the PC, gonna hafta plug in the VGA cable and go into the bios, anyways there’s no approximate about it once I’m done, possibly even the circumference will be exact, though that’s a task for later after I manage to boot up the computer again and upload that code of which I’ve yet to cleanup (had planned on doing it after editing the license)
Seems I had a corrupt partition table that grub couldn’t make sense of, after creating a new one and letting the manjaro installer install with the erase entire disk handler the pc has booted properly now, just need to finish installing various software and copy back all the backed up data then will work on finishing that cleanup and upload the code
You should know that this forum isn’t a blog. We don’t need a daily update complete with a beat-by-beat narration of your difficulties in putting some files on the Internet. It’s OK to post when you’re actually done and there’s actionable information we can look at.
That’s fine, I just figured you’d want to know why I hadn’t uploaded yet, anyways couple more hours time I will start the cleanup and upload here:
I’ve uploaded the base formula, still working on fixing the experimental border calculation (which should also work for ovals), the values are pretty damn close so it’s only a matter of time before I have it right, right now I’d say it’s about 95% correct (didn’t do the math for that percentage but judging by how close the numbers are it sounds about right)
the values are pretty damn close so it’s only a matter of time before I have it right
It is mathematically impossible for you to ever “have it right”. It just can’t happen. Pi is a transcendental number; it cannot be represented exactly in finite space. And the kind of stuff you’re doing could be used to calculate pi. If you ever “had it right”, that would mean you would have a finite function that could calculate pi exactly. Which would mean pi is not transcendental. Which it is.
That’s a contradiction, one that is solved because your attempts to approximate it would only succeed by becoming an infinite series of computations. Which is something we already know.
It’s just an approximation. And not even a good one. It’s not going to magically become better without costing more computational resources.
I have to say, this license is… unique. I’m not a legal expert, but the stuff you added is so wrong that even I can tell.
For example:
As this license apparently gives explicit patent to author of the code (myself) I will not except contributors to this project (because I can’t be bothered with details), this also helps keep the fee system I want on this code simple.
Um, that’s not what the Apache License says. It grants the user of the software a “patent license,” but that just means that any aspects of the software that are covered by a patent are licensed for use by that user. It does not magically grant you a patent; a license can’t do that. Only your country’s patent system can do that. The license is there for when your code is covered by a patent; until you actually have a patent, that section is effectively meaningless.
no operating system, console or other platform and/or hardware that supports running software will be allowed to use the formula in standard functions, instead they must put it in dedicated functions, the prefix and/or suffix I will decide later and name within this document until I die
I don’t believe that telling a user that they must do a specific thing without telling them what that thing is is a valid part of a licensing agreement.
If evidence of foul play is found regarding my future death then the
country which hosted the discovery will recieve double what the below fees would have gotten me from the offender until the day said country determines it is appropriate to release them from said obligation.
You haven’t invented anything novel or world-changing. You merely approximated circles, which people have been doing for centuries. If you tried to patent your algorithm it would likely be refused due to centuries of prior art. And the reason no library like yours exists at present is because there’s no point to it; computers are fast enough to just do better approximations than your “95%” algorithm.
You are not going to be murdered for your code.
- Reserved for any left out scenario’s to be included at a later date (of which will be applicable from the date they are included)
So you reserve the right to just invent a number at some future date, which users of your software will have to pay retroactively all the way back to when they first used the software.
Also, you forgot the copyright date. It still says “Copyright [yyyy] [name of copyright owner]”.
Lastly, the Apache license explicitly states:
each Contributor hereby grants to You a perpetual, worldwide, non-exclusive, no-charge, royalty-free, irrevocable copyright license to reproduce, prepare Derivative Works of, publicly display, publicly perform, sublicense, and distribute theWork and such Derivative Works in Source or Object form.
Emphasis added. Obviously, you are not giving the user such a license. So you shouldn’t claim to be following the Apache License merely “with modifications”.
You’re creating an entirely new license.
Yeah I stopped reading the license about halfway through, anyways no I did not “mean all the way to when they first started using the software” the “applicable from the date they are included” explicitly excludes going back to then - which shows I’m not the only one guilty of not reading properly - anyways, the goal is not to say PI is finite but rather make it simple to calculate it to whatever degree one pleases, another goal is to make it clear that even in physics curves are just an illusion (that one is already proven by the method now), the final goal is to make oval values calculable which I’m sure is of value to the gaming industry at least, no doubt the math community at large too, and possibly the physics community as well, can’t imagine it being all that useful outaide those industries but I’m welcome to being proven wrong on that front. Oh one other point this method proves is that PI is not some intrinsic number of physics or math in general, it’s just a common result of normal math being applied to specfic types of values
Approximating pi and other trig computations is something we’ve been doing for centuries.
I don’t know what it would mean to make “curves” be “just an illusion”. An approximation is just an approximation, and the degree to which your approximation fails to match the actual function is the error term for your function.
While “close enough” may be appropriate in some cases, the existence of “close enough” does not render invalid the actual correct math.
I don’t know what you mean by “calculable”. If you mean that pi actually runs out of digits, or that there can correct, non-transcendental versions of arc math, then your goal isn’t going to be achieved.
Your position reminds me of something that happened in Indiana?
Again, what you’ve done is not new, novel, or different from what has been done for centuries. These communities are not going to transition from using the actual functions to using approximations of them.
That’s contradictory. Pi is an “intrinsic number of physics or math” because it is “just a common result of normal math being applied to specfic[sic] types of values”.
Answering via my phone so will only respond to the last part, just because something is a common result doesn’t make it intrinsic, case in point in pythagorus if you divide C by A you will always get the same result as long as the scale of B divided by A is the same, doesn’t make the number intrinsic just means that if you can arrive at that number without… oh shit I think I just figured that one out
Edit: Nope, idea didn’t work out but I think it is likely along the right lines of what needs to be done to avoid the long square root on C, I just haven’t been able to connect the final dots yet, doing so would
immediately speed up my curvex border math without sacrificing accuracy, the only reason it is currently slower than the PI method is because of the double sqrt, as soon as I can eliminate the lengthy method of obtaining those values (since I always have a & b) then I can throw out sqrt altogether.