Using VBOs to draw a cylinder with selectable faces

OpenGL OpenGL: Basic Coding
1

Hello,

Here is my simple question:

I need to draw a cylinder like the one below using VBOs and cannot use one normal per vertex (need the sharp edges) and need to be able to draw of a different color the three distinct faces (for selection purpose).

What’s the most efficient arrays setup for this purpose? I’ve tested 9 floats X1,Y1,Z1, X2,Y2,Z2, X3,Y3,Z3, 9 floats NX1,NY1,NZ1, NX2,NY2,NZ2, NX3,NY3,NZ3 (36+36=72 bytes per triangle) but it looks so memory-inefficient.

Should I use one VBO per face and use one normal per vertex? What is the overhead if the object has 100s of faces?

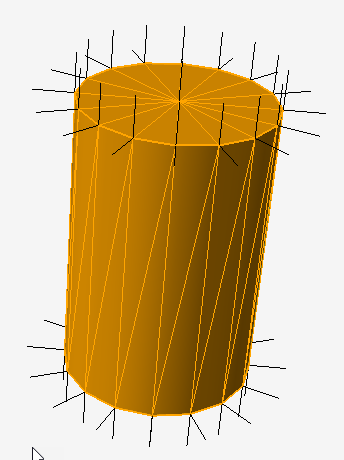
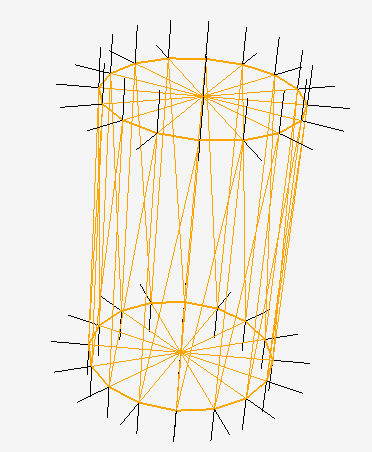
image

Thanks,

Alberto

2

why not? you can have “sharp edges” (“flat shading”) with normal per vertex, you just need to copy a vertex (corner point) with a different normal when it is used to assemble another primitive (with different orientation)

if you thing its too much waste of memory, you can use a geometry shader which calculates the normal

3

You mentioned selection. If this is just for debug/UI (user selection) per-object perf isn’t critical, you might prefer a face normal solution that doesn’t require having to add explicit normals to your vertex attributes, or a special rendering path using a geometry shader. Check out dFdx() and dFdy() in the GLSL spec. These can be used in the frag shader on the position to generate a face normal.

Alternatively, duplicating shared vertices with distinct face normals in your vertex attributes isn’t that expensive. Normals can be as small as 3 bytes per normal, so the overall mem space delta really comes down to the size of your other vertex attribs, and how many shared vertices you have. GPU rendering of meshes in this form is very efficient, as this is standard practice. Probably even more efficient than using a geom shader.

4

It would be really great to see some code/pseudo code for this solution. It’s hard for me to understand how to setup VBO arrays. Suppose for example to have a cube with 4x4=16 vertices per face how should I build vertices, normals and indices (is it necessary?) arrays to duplicate only relevant vertices?

Thanks beforehand,

Alberto

5

If a vertex shader output / fragment shader input has the flat qualifier, the value from the triangle’s last vertex is used for all fragments; the values from the other two vertices are ignored.

Your cylinder has 2N+2 vertex positions but only N+2 normals, so it’s entirely possible to use a single vertex array with 2N+2 vertices.

For the top and bottom faces, the centre vertex should be the last vertex of each triangle, so all triangles will use that normal.

For the vertical faces, use one of the vertices which is shared by both triangles to hold the normal.

vec3 position[2*N+2];
vec3 normal[2*N+2];
uint16_t indices[12*N];

void make_cylinder(float r, float z0, float z1)
{
    position[2*N+0] = vec3(0,0,z0); // top centre
    position[2*N+1] = vec3(0,0,z1); // bottom centre

    normal[2*N+0] = vec3(0,0,-1); // top centre
    normal[2*N+1] = vec3(0,0,1); // bottom centre

    for (int i = 0; i < N; i++)
    {
        float angle = i*2*M_PI/N;
        float x = r*cos(angle);
        float y = r*sin(angle);
        position[2*i+0] = vec3(x, y, z0);
        position[2*i+1] = vec3(x, y, z1);
        float angle2 = angle + M_PI/N; // extra half step
        float nx = cos(angle2);
        float ny = sin(angle2);
        normal[2*i+0] = vec3(nx, ny, 0);
        // normal[2*i+1] isn't used
        int j = (i+1)%N; // index of next face
        // outer faces
        // lower-right triangle
        indices[6*i+0] = 2*j+0; // lower-right
        indices[6*i+1] = 2*j+1; // upper-right
        indices[6*i+2] = 2*i+0; // lower-left; this has the normal
        // upper-left triangle
        indices[6*i+3] = 2*j+1; // upper-right
        indices[6*i+4] = 2*i+1; // upper-left
        indices[6*i+5] = 2*i+0; // lower-left; this has the normal
        // bottom face
        indices[6*N+3*i+1] = 2*j+0;
        indices[6*N+3*i+0] = 2*i+0;
        indices[6*N+3*i+2] = 2*N+0; // centre; this has the normal
        // top face
        indices[9*N+3*i+0] = 2*i+1;
        indices[9*N+3*i+1] = 2*j+1;
        indices[9*N+3*i+2] = 2*N+1; // centre; this has the normal
    }
}

In general, it’s often necessary to have more vertices than vertex positions in order to accommodate all of the normals. Typical triangle meshes have roughly twice as many faces as vertices, meaning that you need to increase the number of vertices to match the number of faces; possibly more, as ensuring that each triangle has at least one unshared vertex is a hard problem for arbitrary triangle meshes. But you don’t need three distinct, unshared vertices per face.

In this case, the number of normals is reduced significantly as all of the triangles on the top and bottom faces share a common normal and both triangles of each edge face share a common normal. So you only have N+2 normals for 4N faces and 2N+2 vertices.

6

GClements,

Mmm… I did my homework and passing these array to OpenGL VBO does not work as I suspected. I tried passing vvv, nnn and indices to VBO and the result is down below. nnn array contains a lot of zeroes. Did I explain myself wrong?

        const int N = 16;

        Point3D[] position = new Point3D[2 * N + 2];
        Vector3D[] normal = new Vector3D[2 * N + 2];

        int[] indices = new int[12 * N];

        const double z0 = 0, z1 = 10;
        const double r = 2;

        position[2 * N + 0] = new Point3D(0, 0, z0); // top centre

        position[2 * N + 1] = new Point3D(0, 0, z1); // bottom centre

        normal[2 * N + 0] = new Vector3D(0, 0, -1); // top centre

        normal[2 * N + 1] = new Vector3D(0, 0, 1); // bottom centre

        for (int i = 0; i < N; i++)
        {

            double angle = i * 2 * Math.PI / N;

            double x = r * Math.Cos(angle);

            double y = r * Math.Sin(angle);

            position[2 * i + 0] = new Point3D(x, y, z0);

            position[2 * i + 1] = new Point3D(x, y, z1);

            double angle2 = angle + Math.PI / N; // extra half step

            double nx = Math.Cos(angle2);

            double ny = Math.Sin(angle2);

            normal[2 * i + 0] = new Vector3D(nx, ny, 0);

            // normal[2*i+1] isn't used

            int j = (i + 1) % N; // index of next face

            // outer faces

            // lower-right triangle

            indices[6 * i + 0] = 2 * j + 0; // lower-right

            indices[6 * i + 1] = 2 * j + 1; // upper-right

            indices[6 * i + 2] = 2 * i + 0; // lower-left; this has the normal

            // upper-left triangle

            indices[6 * i + 3] = 2 * j + 1; // upper-right

            indices[6 * i + 4] = 2 * i + 1; // upper-left

            indices[6 * i + 5] = 2 * i + 0; // lower-left; this has the normal

            // bottom face

            indices[6 * N + 3 * i + 1] = 2 * j + 0;

            indices[6 * N + 3 * i + 0] = 2 * i + 0;

            indices[6 * N + 3 * i + 2] = 2 * N + 0; // centre; this has the normal

            // top face

            indices[9 * N + 3 * i + 0] = 2 * i + 1;

            indices[9 * N + 3 * i + 1] = 2 * j + 1;

            indices[9 * N + 3 * i + 2] = 2 * N + 1; // centre; this has the normal

        }

        float[] vvv = new float[position.Length*3];

        for (int i = 0; i < position.Length; i++)
        {
            vvv[i * 3 + 0] = (float)position[i].X;
            vvv[i * 3 + 1] = (float)position[i].Y;
            vvv[i * 3 + 2] = (float)position[i].Z;
        }

        float[] nnn = new float[normal.Length * 3];

        for (int i = 0; i < normal.Length; i++)
        {
            if (normal[i] == null) continue;

            nnn[i * 3 + 0] = (float)normal[i].X;
            nnn[i * 3 + 1] = (float)normal[i].Y;
            nnn[i * 3 + 2] = (float)normal[i].Z;
        }

Resulting VBO mesh:
image

7

That image doesn’t look flat-shaded. Use glShadeModel(GL_FLAT) for the fixed-function pipeline; if using shaders, use the flat qualifier on the fragment shader input variable for the normal.

Also, ensure that the light position is outside of the cylinder; preferably somewhere between the cylinder and the viewpoint (otherwise you’ll be lighting the side you can’t see).

That’s correct. There are 2N+2 vertices but only N+2 distinct normals (where N is the number of angular divisions), so the normal array has many unused entries (all attribute arrays must be the same size, so you can’t just have a smaller array for the normals).

8

Again, I need averaged normals on the vertical triangle strip and want to represent sharp edges on circular edges. Can you please add to your code the VBO calls to setup arrays and verify that it’s working?

So far I can only obtain the proper drawing using:

9 floats X1,Y1,Z1, X2,Y2,Z2, X3,Y3,Z3, 9 floats NX1,NY1,NZ1, NX2,NY2,NZ2, NX3,NY3,NZ3 (36+36=72 bytes per triangle)

Repeating vertices and normals for each triangle, it’s soo memory inefficient…

I just want to be sure that there aren’t other options… Here are two pictures that explain what normals we need. What the most efficient VBO setup to get this result?

image image

Thanks,

Alberto

9

In that case, you can’t use flat-shading. The triangles on the top and bottom faces can share the centre vertex, can share the edge vertices with other triangles on the top and bottom faces, but can’t share the edge vertices with the faces on the outside of the cylinder.

So you need 4N+2 vertices: N+1 on the top, N+1 on the bottom, 2N on the outside.

vec3 position[4*N+2];
vec3 normal[4*N+2];
uint16_t indices[12*N];

void make_cylinder(float r, float z0, float z1)
{
    position[4*N+0] = vec3(0,0,z0); // top centre
    position[4*N+1] = vec3(0,0,z1); // bottom centre

    normal[4*N+0] = vec3(0,0,-1); // top centre
    normal[4*N+1] = vec3(0,0,1); // bottom centre

    for (int i = 0; i < N; i++)
    {
        float angle = i*2*M_PI/N;
        float nx = cos(angle);
        float ny = sin(angle);
        float x = r*nx;
        float y = r*ny;
        position[2*i+0] = position[2*N+i] = vec3(x, y, z0);
        position[2*i+1] = position[3*N+i] = vec3(x, y, z1);
        vec3(nx, ny, 0);
        normal[2*i+0] = vec3(nx, ny, 0);
        normal[2*i+1] = vec3(nx, ny, 0);
        normal[2*N+i] = vec3(0, 0,-1);
        normal[3*N+i] = vec3(0, 0, 1);

        int j = (i+1)%N; // index of next face
        // outer faces
        // lower-right triangle
        indices[6*i+0] = 2*j+0; // lower-right
        indices[6*i+1] = 2*j+1; // upper-right
        indices[6*i+2] = 2*i+0; // lower-left
        // upper-left triangle
        indices[6*i+3] = 2*j+1; // upper-right
        indices[6*i+4] = 2*i+1; // upper-left
        indices[6*i+5] = 2*i+0; // lower-left
        // bottom face
        indices[6*N+3*i+1] = 2*N+j;
        indices[6*N+3*i+0] = 2*N+i;
        indices[6*N+3*i+2] = 4*N+0; // centre
        // top face
        indices[9*N+3*i+0] = 3*N+i;
        indices[9*N+3*i+1] = 3*N+j;
        indices[9*N+3*i+2] = 4*N+1; // centre
    }
}
10

Thanks GElements,

Please include the code to initialize the VBO arrays, I cannot understand how normal are linked to indices. I need to see your code working with VBOs.

Thanks beforehand,

Alberto

11

Stop worrying about this, you’re pre-emptively micro-optimizing something that isn’t even as important as you think it is.

I’ll repeat this.

For the amount of data you’re using here, a few extra bytes per vertex is not as important as you think it is.

If you were storing millions of cylinders in your buffer, then we might talk about strategies for reducing memory usage. But you haven’t indicated that you’re doing so, so stop worrying about it, stop wasting time and energy on things that don’t even matter, and direct your efforts towards optimizations that will actually give results.

12

We have meshes with 1.000.000 vertices/triangles and duplicating makes “some” difference.

I repeat the question again: is there any way to optimize VBOs for this problem or not?

Thanks,

Alberto

13

Position and normal are attribute arrays, indices is the element array. Assuming position/normal attribute locations are 0 and 1 respectively:

    glGenBuffers(1, &position_buf);
    glBindBuffer(GL_ARRAY_BUFFER, position_buf);
    glBufferData(GL_ARRAY_BUFFER, (4*N+2)*3*sizeof(GLfloat), (const void*) position, GL_STATIC_DRAW);
    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, (const void *) 0);
    glEnableVertexAttribArray(0);

    glGenBuffers(1, &normal_buf);
    glBindBuffer(GL_ARRAY_BUFFER, normal_buf);
    glBufferData(GL_ARRAY_BUFFER, (4*N+2)*3*sizeof(GLfloat), (const void*) normal, GL_STATIC_DRAW);
    glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 0, (const void *) 0);
    glEnableVertexAttribArray(1);

    glGenBuffers(1, &index_buf);
    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, index_buf);
    glBufferData(GL_ELEMENT_ARRAY_BUFFER, 12*N*sizeof(GLushort), (const void*) indices, GL_STATIC_DRAW);

    ...

    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, index_buf);
    glDrawElements(GL_TRIANGLES, 12*N, GL_UNSIGNED_SHORT, (const GLvoid*) 0);

PS: if you’re concerned about size, consider using GL_BYTE or GL_INT_2_10_10_10_REV for the normal array. You don’t need three 32-bit floats for a normal. You can even get normals down to 16 bits without significant loss of accuracy at the expense of some computation (or a table lookup) in the vertex shader (bear in mind that you don’t normally care about the magnitude, so normals are effectively two-dimensional).

14

You have 1 million triangle models that are flat-shaded?

Flat-shading is not especially common in real-life models.

It is not a problem that requires optimization. You just accept that you need to do it, and if mesh size is really a problem, consider using smaller mesh data.

15

It appears he wasn’t actually after flat-shading, but sharp edges.

16

That’s correct, no FLAT shading.

Ok, so I need to duplicate everything. Just wanted to be sure. This also poses a limit when you need to update vertices in real time, like for drawing the sea surface that changes at every frame. At every frame you need to convert a compact representation in this critical data duplication.

Thanks a lot for your help.

Alberto

17

No, you only need to duplicate things at sharp edges. A position is only shared by two or more triangles if all of the attributes of that vertex (position, normal, etc) are the same. If any are different, then the other attributes must be duplicated.

That would only be needed if the undulations are expected to create hard edges.

And if you’re in a circumstance where you’re generating mesh data every frame that will dynamically modify its topology, I would seriously consider using buffer textures/SSBOs and manual multiple indexing rather than vertex attributes.

18

No, you only need to duplicate things at sharp edges. A position is only shared by two or more triangles if all of the attributes of that vertex (position, normal, etc) are the same. If any are different, then the other attributes must be duplicated.

It would really help a small code sample about this, even with three triangles: two touch on a smooth (averaged normal) edge and two with a sharp edge (each triangle has its own normal).

19

You already have a code example for the cylinder.

I think you’ll need to explain exactly what part you don’t understand. When you have a sharp edge, you need to duplicate all vertices on that edge. A “vertex” only has a single normal, so if you have a single position with two different normals, that’s two vertices.

It’s possible to create meshes using an OBJ-like format, where you have arrays for position and normal data and faces are defined with “vertices” which contain an index for the position and another index for the normal. However, there’s a definite performance cost for this (performing array lookups in the vertex shader is more expensive than using vertex attributes as the latter can be pipelined while the former is constrained by memory-access latency) and it typically requires more space than duplicating vertices (because you now have to store two indices for every vertex, as well as the position and normal data). It’s only worthwhile if most vertices are on a sharp edge (or texture seam, if you have texture coordinates).

20

OBJ-like is a good example and let’s keep shaders out of the game: how do you filter vertices on a face boundary from the ones in the face middle? To determine what to duplicate and what not?

Thanks,