Software near and far clipping

OpenGL
1

This is actually for a software renderer, but since my plan is to have it accept the same input and produce the same(ish) output as GL, I thought this might be a good place to ask.

I’m trying to add clipping to the rasteriser, mostly from http://omega.di.unipi.it/web/IUM/Waterloo/node51.html . So far I have left/right/top/bottom clipping working ok, and I can classify if a point is beyond the near plane by using (clip.z < -clip.w), but I’m stuck when it comes to actually clipping against the near and far planes. Unfortunately that document doesn’t give the equation for the near and far planes.

I also found another paper ( http://www.unchainedgeometry.com/jbloom/pdf/homog-coords.pdf ) that has equations for all six planes (right at the bottom of page 22), but I don’t understand the near and far plane equations, or how they’ve been derived. Also they give really odd results which I can’t make sense of.

Could someone tell me where (in gl clip space) the near plane actually lies? All I’ve been able to gather is that it’s at z=w, which makes sense to me for classifying, but I don’t know how I can clip to it without first doing the w divide, which then causes weird sign flips.

Thanks.

2

ignore the weird sign flips, look at region “2” here:

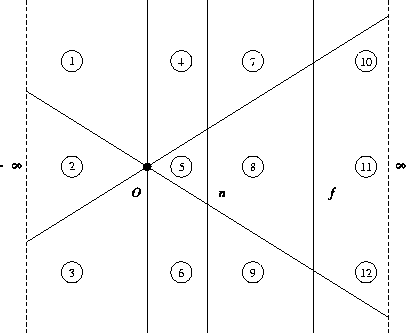
Even if you remove the near clipplane, the left/right/top/bottom planes will clip anything behind the camera ( O ).

So safely clip when z is out of the range (-w;w)

3

So if I follow you, the left/right/top/bottom planes will clip down to regions 5, 8 and 11, so I just need to focus on the range between 0-n to clip the near plane?

However that still leaves me confused - how do I clip to (-w;w)? I don’t understand how that represents a plane. What is w in this context as I have two completely different w values for each point at each end of my line to clip.

Thanks

4

(-w;w) represents two planes that you’re directly looking at. As in, dot(planeNorm, eyeDir) = 1 or -1;

You clip by comparing the point’s z to its w, not by comparing different points’ w values.

5

You clip by comparing the point’s z to its w, not by comparing different points’ w values.

That’s just a visible/not-visible test; that’s not clipping. All three points of a triangle could be non-visible, but part of the triangle could still be on-screen.

6

True, I dumbed-down that sentence; just wanted to state he shouldn’t compare different W values among themselves. Instead, z against w in interpolated z:w pairs .

7

I think I see. So if I ignore the x & y components, then the actual near plane is at (w-z=0) ?

So, following the same method at the bottom of http://omega.di.unipi.it/web/IUM/Waterloo/node51.html , I can start from the P=(1-a)P0 + aP1 equation, rearrange to solve for a, then use the w and z coords from the line end points to find a, which I can then use to find the actual intersection point with the near clip plane.

Is there anything I’ve missed here? It seems correct, so I’m going to try it and see where it fails. :slight_smile: