Not even sure if anyone is still following this thread anymore. Really hope so because I’m really close on to something but not sure how to overcome a small hurdle.
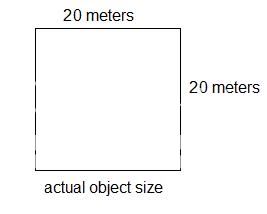
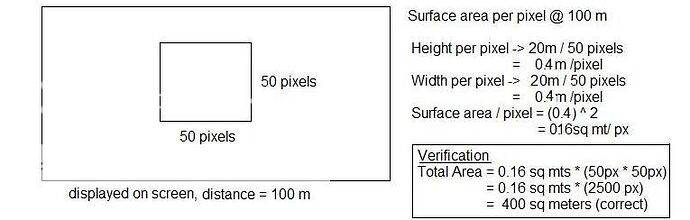
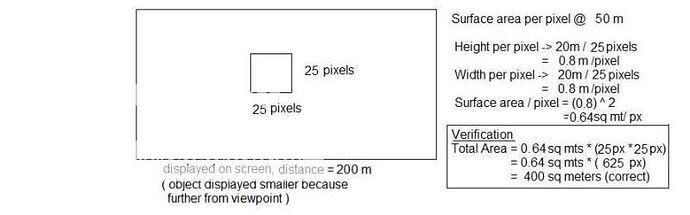
Once I knew that a fragment was always one pixel, the surface area per fragment was fairly simple. If the object was of size NxN (for simplicity), measure the number of pixels the object takes up in one direction at a given distance, call it P. The width per pixel should roughly be N/P. ie. if the object is 10 meters x 10 meters, and is represented 100 px x 100 px on the screen, each pixel represents 0.1 meter horizontally and 0.1 meter vertically, or 0.01 sq meters (reversing the process, 0.01 sq meters * (100x100) = 100 sq meters, the original surface area.
A crudely simplistic example but enough that repeating it over a sample of several dozen distances I was able to develop a linear trend line (distance * constant) that accurately predicted the per pixel surface area within a few decimal places for several ranges. (We’d actually like to get it down to lower than this if possible, and hopefully what I get to next will help with that).
The problem becomes when the object is placed at the extrema of its visibility. Say the object stops being visible at distance D. Prior to that, the object remains at a size of some small MxM (in this case, 2x2) for a significant amount of time, meaning the surface area per pixel remains the same (plateaus more or less) over this span until the object disappears. (It actually starts to spike and plateau before this a little but this is where it gets extreme.)
So the problem is that toward the end of visibility an object no longer follows this trend line, and while this would be okay if we were only representing this NxN test object, obviously we’re representing tons of objects and have no way of knowing in the fragment shader what object we’re working on. So while an NxN object will depart from the trend line at some distance D-delta, an object of size 2Nx2N might not depart from the trend line until something like 2D-delta (or something close, I haven’t done the exact math on that part).
I’m PRETTY SURE the reason for the plateau is that when the object is placed at an extreme distance, it starts taking up fractions of pixels, something like 1.75px x 1.75px and gets rounded up to 2x2, then move it back and it becomes 1.66px x 1.66px and gets rounded up to 2x2, until eventually it reaches 1x1 and eventually disappears.
The only solution to this problem I can think of is to check if a pixel is a partial pixel, if GLSL contains any kind of support for this, but I would imagine which pixels were on and which were off would already have been determined in the vertex shader (just a guess, I’m not especially great at this…)
I don’t really know what else could be done. Any guidance / advice would be GREAT at this point.
EDIT: as an aside, we’d like to try and avoid using antialiasing if at all possible for speed reasons. But if that’s the only way to achieve this… then maybe we’ll have to switch over to that.