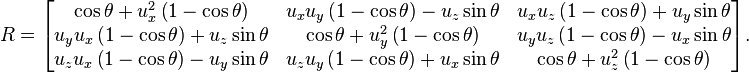I need some clarification about glRotatef function. I have a rectangular plane with normal ax + by + cz = 0;
I would like to rotate it along (0, 1, 0) i.e. Y-axis.
I can find the in-between angle by dot product. Suppose the angle is theta in degree. Now how can I use glRotatef function to rotate the plane so that the new normal to the plane is along (0, 1, 0) vector; Is the following ok?
glRotatef( - theta, a, b, c);
If not, what will be the correct version?
That is not correct. It is not quite clear what you want to achieve.
-
If you want to make plane’s normal to be coincident with Y-axis, then you need to find axis around which you have to rotate a plane. The angle is correct. It can be calculated from the scalar product. The axis, or to be more precise, the vector of rotation can be calculated from vector product: (nx, ny, nz) = (a,b,c) x (0,1,0).
=> glRotatef(teta, nx, ny, nz) -
If the rotation should be done around Y-axis => glRotatef(alpha, 0, 1, 0). But for which angle, it is not defined by the question. So, this assumption is probably wrong.
Thank you. The first one is what I asked. But whether it would be glRotatef( -theta, nx, ny, nz) or glRotatef( +theta, nx, ny, nz) . Could you explain a bit?
Could you let me know how to find out the corrsponding rotation matrix in this case?
I found the following link helpful:
Rotation matrix from axis and angleFor some applications, it is helpful to be able to make a rotation with a given axis. Given a unit vector u = (u[SUB]x[/SUB], u[SUB]y[/SUB], u[SUB]z[/SUB]), where u[SUB]x[/SUB]2 + u[SUB]y[/SUB]2 + u[SUB]z[/SUB]2 = 1, the matrix for a rotation by an angle of θ about an axis in the direction of u is